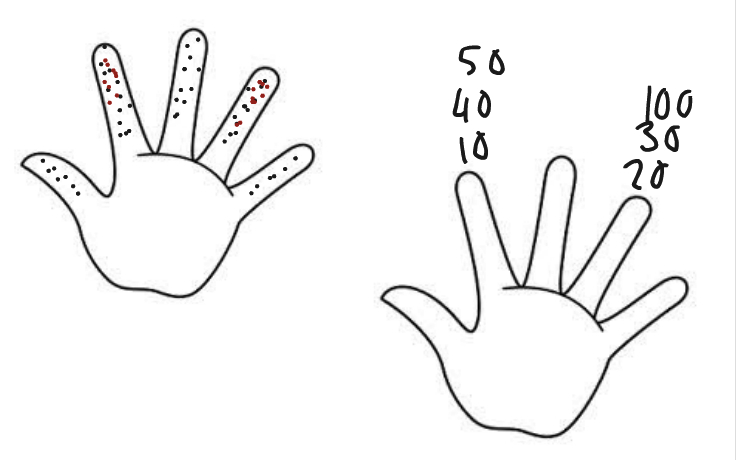
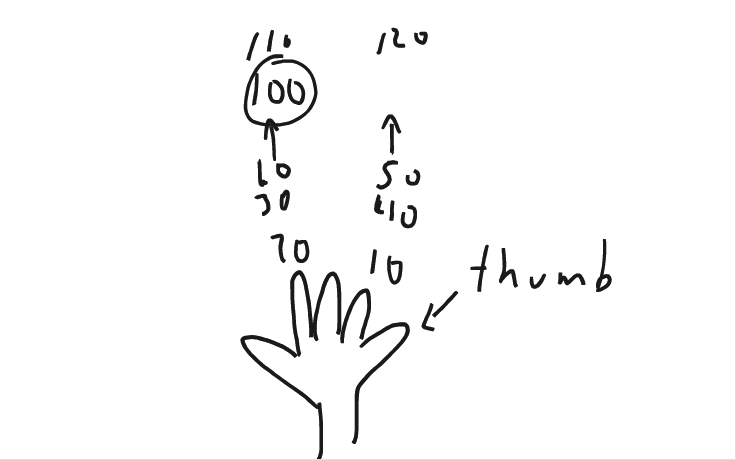
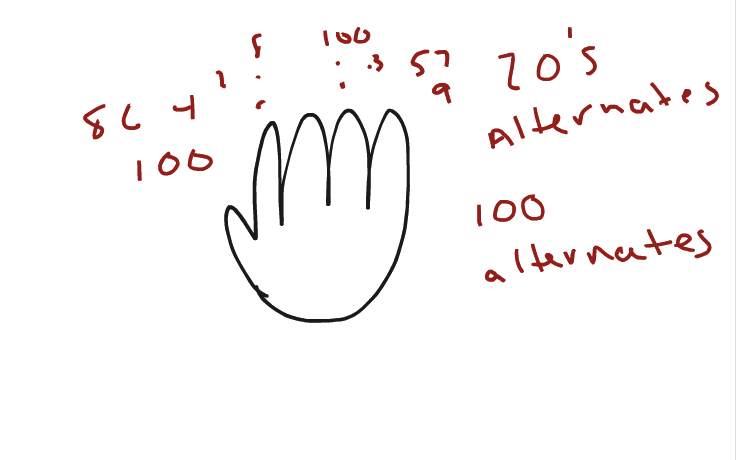
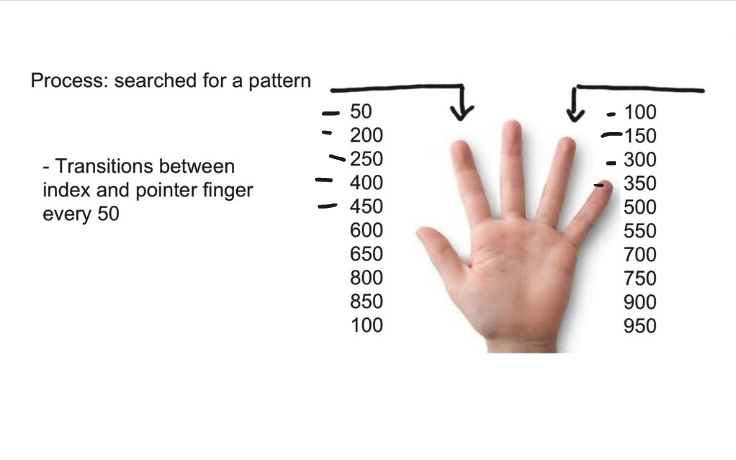
Challenge 03: Finger Counting
[Back to the Archive]
|
|
|
Video Responses
Spoiler Alert! Video responses include explanations of how to solve the challenge problem. We recommend that you resist the temptation to watch response videos until after you have explored the challenge individually or with a problem solving team!
Video Responses: Group A
Andrea & Sara's solution.
|
Ashlyn's solution.
|
Don's solution.
|
Ginny's solution.
|
Kendall's solution.
|
Wynne's solution.
|
Video Responses: Group B
Jared's solution.
|
Logan's solution.
|
Nathan's solution.
|
Nathaniel's solution.
|
Shelby, Tasha, & Tommy's solution.
|
Video Responses: Group C
|
Chris's solution.
|
Kaylyn's solution.
|
Maile's solution.
(Click here for more about this solution.) |
Paul's solution.
|
Follow-up Challenges
- Compare the videos in each group. What features are shared among the solutions in the same group? What features make the groups different from each other? Would you propose a different grouping?
- Don's solution is like the others in Group A and he gets the same answer, but there's a problem in the way he extends his pattern. What's the problem? Why does he still get the right answer?
- Ginny's solution is also like the others in Group A, but there's a problem that leads her to a different answer. What's the problem? Compare her problem and Don's. How are they the same, how are they different?
- Nathaniel notes that there are "five 20s in 100". How does this factor in to his solution? Can we apply this same kind of reasoning to solve the challenge in other ways?
- Compare Chris's and Kaylyn's solutions. How are they the same? How are they different? What advice would you give to Kaylyn?
- Describe Maile's approach in your own words. Does it always work? Can we use her strategy to determine which finger you will end on when counting up to the number 110?
- Explore Paul's approach, which introduces the idea of modular arithmetic.
